introduction

Dans le domaine des transferts thermiques, il existe de nombreux ouvrages qui présentent les notions théoriques fondamentales. Les problèmes académiques qui y sont traités ont généralement des solutions analytiques s'exprimant le plus souvent sous forme de séries infinies où apparaissent parfois des fonctions particulières (fonctions de Bessel, fonction erreur …)
FlashTherm est un outil informatique qui vient compléter ces ouvrages. Il permet à l'utilisateur de mettre en évidence par la simulation, les aspects fondamentaux du phénomène de conduction thermique (notions d'inertie et de profondeur de pénétration par exemple).
résumé

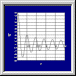 |
Flashtherm comporte un outil vous permettant de vous familiariser avec un certain nombre de fonctions particulières souvent utilisées en thermique (fonctions de Bessel, fonction erreur ..)
|
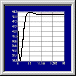 |
Mur semi-infini en régime périodique: Utilisation des fonctions erreur et erreur complémantaire pour résoudre le problème du mur semi-infini soumis à un échelon de température ou de flux |
 |
Ailettes de section uniforme: Résolution du problème de l'ailette en considérant plusieurs cas de conditions aux limites (convection au bout de l'ailette, bout de l'ailette adiabatique etc.) |
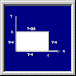 |
Régime stationnaire bidimensionnel: Problème du cylindre de section rectangulaire de côtés a et b dont l'une des faces est à une température f(x) et les trois autres sont maintenues à une tempé nulle. |
 |
Capacité: La notion de capacité thermique est basée sur l'hypothèse d'isothermie d'un corps. Elle conduit à une loi exponentielle d'évolution. La comparaison de la solution donnée par cette hypothèse à la solution analytique dans le cas d'une sphère permet de déduire les limites de validité de cette hypothèse |
 |
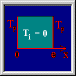
Calcul du temps de demi-chauffe: Détermination du temps de demi-chauffe d'une sphère initialement à une température Ti et subitement portée à une température Tb en surface. Le temps de demi-chauffe est le temps nécessaire pour que l'écart entre la température en un point de la sphère et la température imposée soit divisé par deux. |
 |
Méthode des fonctions de transfert approchées: Etude d'un mur soumis à une température constante Tp. La solution en x = L / 2 dans le domaine de Laplace permet de déduire des fonctions de transfert approchées d'ordre 1 et 2 facilement inversible… |
 |
Théorème de Duhamel: Ce théorème permet de déterminer l'évolution des températures dans un milieu, sous l'influence de sollicitations variables dans le temps, si l'on connaît l'évolution des températures correspondant à des sollicitations constantes. Ce théorème est illustré à travers l'exemple de la conduction dans un mur d'épaisseur L. |
 |
Méthode intégrale: Les méthodes intégrales sont généralement utilisées dans le cas
de transferts unidimensionnels linéaires ou non. Elles utilisent la notion de profondeur de pénétration d(t) définissant une couche thermique au delà de laquelle le flux de chaleur est pratiquement nul. << Rappel et exploitation des fondements mathématiques de la méthode. |
 |
Mesure de la diffusivité thermique par la méthode flash: Etude d'un mur soumis à une température constante TpLa plupart des méthodes de mesure de la diffusivité des solides isotropes sont basées sur des techniques impulsionnelles. Mise en œuvre et illustration des notions théoriques nécessaires à la modélisation du phénomène. |
![]()
![]()