![]()
![]()
I. INTRODUCTION
La recherche des solutions de problèmes de conduction par la méthode des transformées de LAPLACE seffectue en trois étapes :
ü Ecriture de léquation transformée du problème
ü Résolution de cette équation transformée
ü Retour à la solution physique par application du théorème dinversion ou par utilisation de tables de transformée de Laplace.
Lexemple dun mur soumis à une température constante Tp sur ses deux faces est considéré dans ce TP. La solution en x = L /2 dans le domaine de LAPLACE appelée fonction de transfert permet de déduire des fonctions de transfert approchées dordre 1 et 2 facilement inversibles. Ceci conduit à des solutions approchées du problème qui sont comparées à la solution analytique exacte.
II. POSITION DE PROBLEME
On considère léquation de la chaleur dans un mur dépaisseur e et de diffusivitéa :
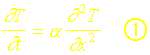
Les deux faces du mur sont soumises à une température initiale f(t) de sorte que lon peut écrire :
![]()
On supposera enfin que le mur est à une température initiale T(x,0) = 0
III. FORMULATION DANS LE DOMAINE DE LAPLACE
On utilise la transformation de LAPLACE pour résoudre ce problème. Désignons respectivement par q (x,p) et F(p), les transformations de Laplace de T(x,t) et de f(t)
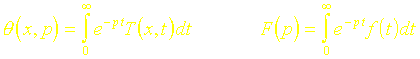
Effectuons à présent la transformation de Laplace sur les deux membres de léquation :
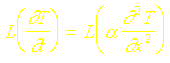
Les propriétés de linéarité de lopérateur L (qui désigne la transformation de Laplace ) permettent décrire :
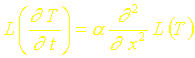
Or:
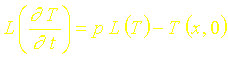
Sachant que T(x,0)=0 on a donc :
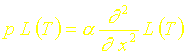
Soit:
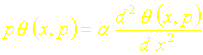
Les conditions aux limites sécrivent quant à elles :
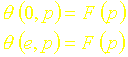
La résolution de léquation différentielle du second ordre précédente conduit à :
![]()
Où les deux constantes dintégration C1 et C2 sont déterminées par les conditions aux limites. On a en effet :
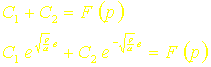
Soit:
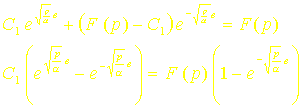
Ou encore:
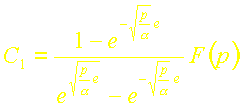
Or:
C2 = F(p) - C1
Donc:
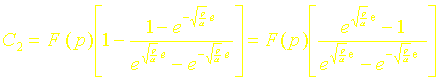
La transformée de la température sécrit donc :
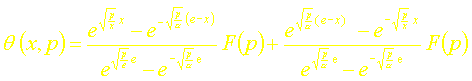
Soit:
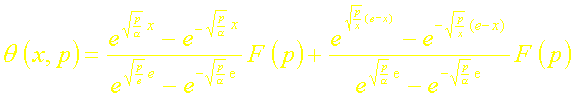
En introduisant la fonction Sinus hyperbolique, ceci sécrit :
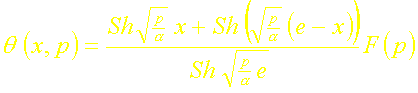
IV. FONCTION DE TRANSFERT
On définit la fonction de transfert H(x,p) à une abscisse x, comme étant le rapport dans le domaine de Laplace de la réponse q (x,p) à la sollicitation F(p).
Elle sécrit donc :
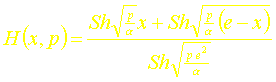
La transformation inverse de la fonction de transfert conduit à la réponse impulsionnelle du système linéaire considéré.
![]()
La réponse à un échelon on à toute autre excitation variable sen déduit par intégration (théorème de DUHAMEL).
V. FONCTIONS DE TRANSFERT APPROCHEES
La fonction de transfert précédente est difficilement inversible. Nous allons donc chercher à lapprocher en utilisant le fait que la fonction sinh est développable en série entière toujours convergente :
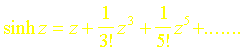
En remplaçant dans lexpression de la fonction de transfert, le sinus hyperbolique par les deux premiers termes de son développement, on obtient la fonction de transfert approchée à lordre un suivante :
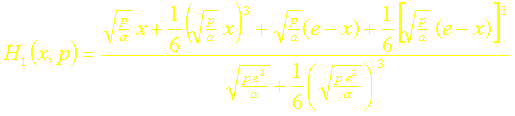
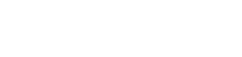
![]()
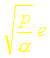
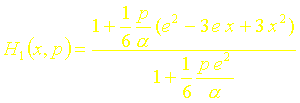
La fonction de transfert approchée à lordre un sécrira donc au centre du mur ( x = e/2 ) :
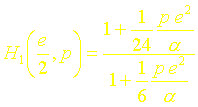
En considérant les trois premiers termes du développement en série du sinus hyperbolique, on montre de la même manière que la fonction de transfert approchée à lordre deux au centre du mur (x=e/2) sécrit :
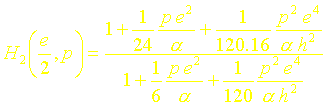
VI. REPONSES IMPULSIONNELLES ET REPONSES INDICIELLES
Les fonctions de transfert approchées précédentes sécrivent sous la forme générale :
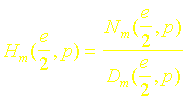
Afin de pouvoir effectuer facilement le retour vers lespace physique, nous allons effectuer une division polynomiale suivant les puissances croissantes de p et écrire :
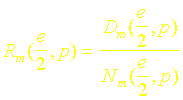
La fonction de transfert sécrira donc sous la forme plus classique :
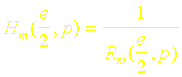
où Rm est un polynôme du premier ou du second degré.
On montre alors que :
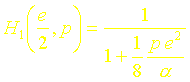
ce qui sécrit aussi :
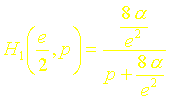
La réponse impulsionnelle à lordre un est donc simplement :
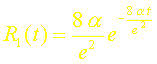
La réponse indicielle ou réponse à un échelon sen déduit par simple intégration :
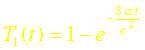
A lordre deux, la division polynomiale conduit à :
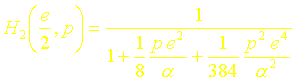
soit encore :
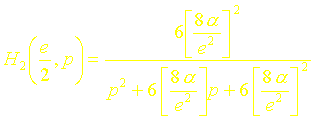
Les pôles de cette fonction de transfert dordre deux sont :

soit :

On peut donc écrire :
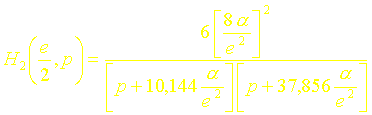
La réponse impulsionnelle à lordre deux sen déduit :
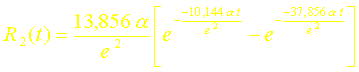
La réponse à un échelon sera donc ici :
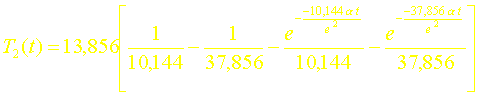
VII. DEROULEMENT DU TP
A. Développements analytiques
Ø Déterminer les fonctions de transfert approchées dordre un et deux en fonction de x.
Ø Calculer les pôles de ces fonctions en fonction de x.
v En déduire le domaine de validité du modèle dordre deux.
B. Expérience numériques
Ø Effectuer des simulations pour différents matériaux et différentes épaisseurs
Ø Effectuer une simulation en utilisant des grandeurs adimensionnelles
v En déduire le domaine temporel de validité de ces solutions approchées en utilisant le nombre de FOURIER
v Quelle épaisseur doit avoir une plaque de cuivre pour que la solution dordre deux soit correcte à partir de 4 secondes ?
v Quelle épaisseur doit avoir une plaque de béton pour que la solution dordre deux soit correcte à partir de 15 minutes ?
![]()