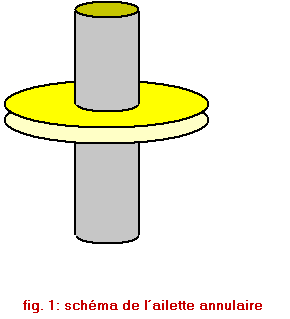
On se propose d’étudier dans ce TP l’efficacité d’une ailette annulaire. On utilisera pour cela les fonctions de BESSEL. La figure 1 représente une ailette annulaire d’épaisseur e de rayon intérieur r_i et de rayon extérieur r_e . Le fluide est à une température T_f  et le cylindre intérieur est à une température T_o . On désignera par  h  le coefficient d’échange et par q  la différence de température q =T - T_f.

1.  En effectuant un bilan d’énergie, montrer que l’équation différentielle qui régit la température q  s’écrit :

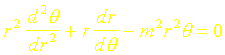
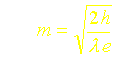
2.  L’équation précédente est une équation de Bessel modifiée d’ordre 0. Sa solution générale est donc :

On supposera que les conditions aux limites sont :

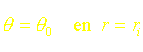
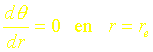
Montrer alors que ces conditions conduisent aux relations suivantes :

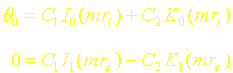
On rappelle que l’on a :

3.  Montrer que la relation exprimant la répartition de température dans l’ailette est :

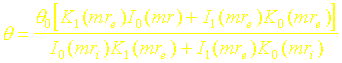
4.  En déduire que le flux de chaleur s’exprime sous la forme :

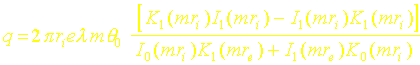
5.  En l’absence d’ailette, le flux évacué sur l’épaisseur e serait égal à:

6.  On peut ainsi définir l’efficacité de l’ailette par le rapport e :

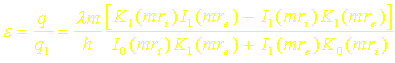
On définit également le rendement h de l’ailette par le rapport entre le flux évacué par l’ailette au flux  q₂  qu’elle aurait évacué si elle était portée entièrement à la température de la base q₀ .

En négligeant l'épaisseur de l'ailette, ce flux s'écrit:

Le rendement est donc ici :

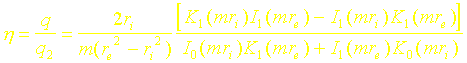
7.  Exercice d’application :

On veut réaliser une ailette annulaire avec r_i = 1cm, r_e = 2cm, e = 1mm. Le coefficient d’échange est de  25 W/m²K.

Calculer le rendement dans les cas où le matériau choisi est :

v de l’aluminium [ l=238 W/mK ]

v du cuivre [ l=394 W/mK ]

v du fer [ l=73 W/mK ]

Réponse : Les rendements sont successivement de :

h_AL=0.98866   h_CU=0.99266   h_FE=0.9928

Problème : Effectuer la même étude dans le cas d’une ailette triangulaire