![]()
![]()
I. FONCTIONS ERREUR ET ERREUR COMPLEMENTAIRE
Les fonctions erreur (erf ) et erreur complémentaire (erfc) qui interviennent dans l’étude du mur semi-infini sont définies par :
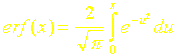
![]()
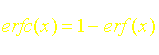
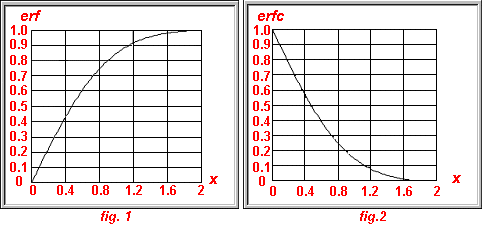
Ces fonctions représentées sur les figures 1 et 2 sont calculées par le logiciel à l’aide du développement en série suivant :
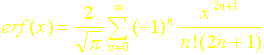
remarque : le nombre de termes est limité à 170
II. FONCTIONS DE BESSEL
L’équation différentielle (1) est appelée équation différentielle de BESSEL d’ordre n.
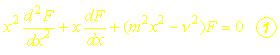
Sa solution générale s’écrit sous la forme :![]()
![]()
où Jn et Yn sont respectivement les fonctions de Bessel d’ordre n de première et de deuxième espèce.
L’équation (2) est appelée équation différentielle modifiée de BESSEL d’ordren.
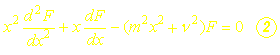
Sa solution générale s’écrit sous la forme :![]()
![]()
où In et Kn sont respectivement les fonctions de Bessel modifiées d’ordre n de première et de deuxième espèce. Ces fonctions de BESSEL jouent un rôle fondamental en conduction quand la géométrie est cylindrique. On donne dans les paragraphes suivants les expressions qui permettent de les calculer.
A. Fonctions de BESSEL de première espèce d’ordre 0 et 1
Ces fonctions représentées sur les figures 3 et 4, sont calculées en utilisant les développements en série suivants :
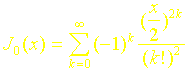
![]()
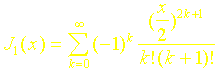
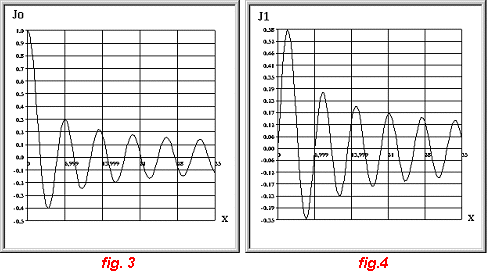
remarque : En raison des dépassements de capacité, ces fonctions ne peuvent être tracées que pour une valeur de x maximum égale à 35. Le nombre de termes de la série doit être de 98 au voisinage de cette valeur maximum.
B. Fonctions de BESSEL de deuxième espèce d’ordre 0 et 1
Les Fonctions de BESSEL de deuxième espèce d’ordre 0 et 1 sont calculées grâce aux relations suivantes :
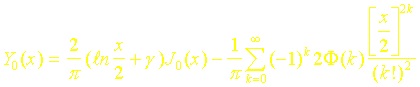
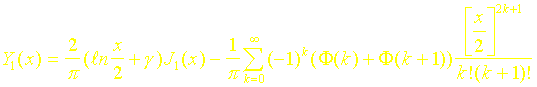
où F(k) représente la série:
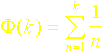
et où g est le nombre d'EULER ( g = 0,5772156649 ). Elles sont représentées sur les figures 5 et 6.
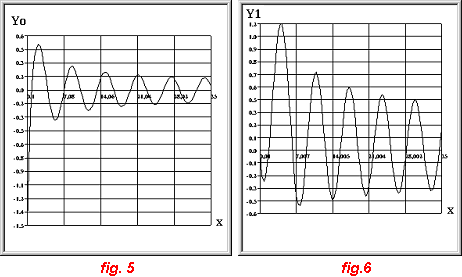
remarque : En raison des dépassements de capacité, ces fonctions ne peuvent être tracées que pour une valeur de x maximum égale à 35. Le nombre de termes de la série doit être de 98 au voisinage de cette valeur maximum.
C. Fonctions de BESSEL modifiées de première espèce d’ordre 0 et 1
Ces Fonctions Ces fonctions sont représentées sur les figures 7 et 8 et sont calculées par utilisation des développements :
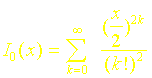
![]()
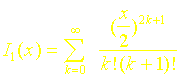
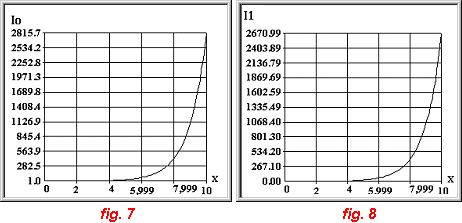
remarque : Le nombre de termes est ici limité à 20.
D. Fonctions de BESSEL modifiées de deuxième espèce d’orde 0 et 1
Les Fonctions de BESSEL modifiées de deuxième espèce d’ordre 0 et 1 sont calculées grâce aux relations suivantes :
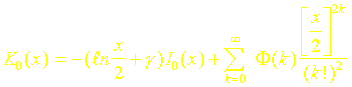
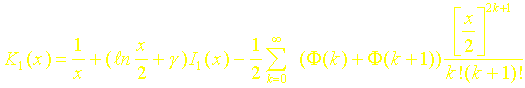
où F(k) représente la série:
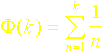
et où g est le nombre d'EULER ( g = 0,5772156649 ). Elles sont représentées sur les figures 9 et 10.
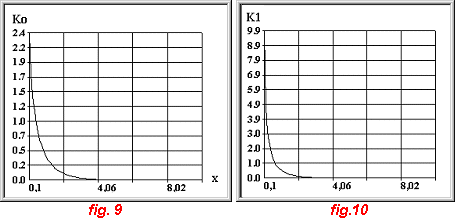
remarque : Le nombre de termes est ici limité à 20.
E. Approximations des fonctions de BESSEL modifiées de deuxième espèce
Les expressions précédentes donnant K0(x) et K1(x) convergent lentement. On préfère alors utiliser les approximations suivantes :
- pour 0 < x £ 2
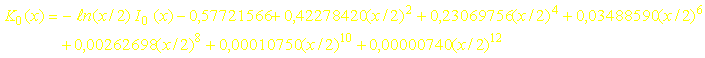
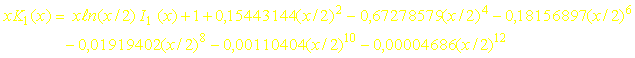
- pour 2£ x < ¥
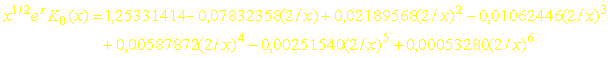
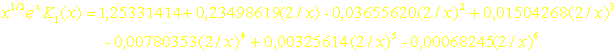
![]()