![]()
![]()
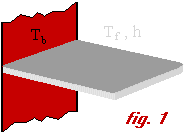
En effectuant le changement de variables q =T-Tf , l’équation différentielle qui permet de résoudre le problème de l’ailette de section uniforme S et de périmètre P {Figure 1} s’écrit :
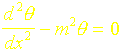
où
![]()
h et l représentant respectivement le coefficient d’échange et la conductivité thermique du solide. La base de l’ailette étant à la température du mur Tb, la solution dépend en définitive de la condition aux limites imposée au bout de l’ailette de longueur L.
I. Cas où l’on considère la convection au bout de l’ailette
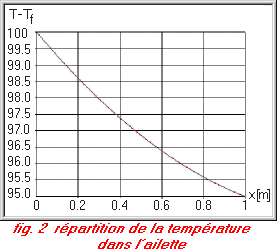
Dans le cas où l’on considère la convection au bout de l’ailette, la répartition de température représentée sur la figure 2 et le flux de chaleur évacué par l’ailette sont donnés par les relations:
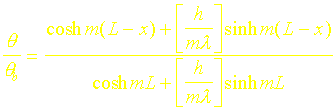
![]()
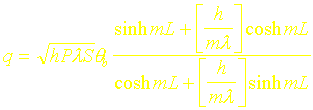
II. Cas où l’on considère le bout de l’ailette adiabatique
Si l’on considère le bout de l’ailette comme étant adiabatique, les expressions précédentes deviennent:
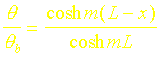
![]()
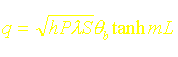
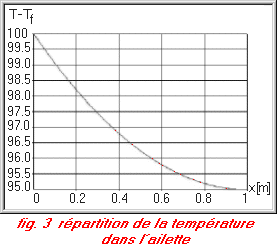
III. Cas où l’on impose la température au bout de l’ailette q(L) = qL
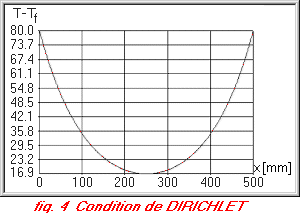
Dans certaines situations, le bout de l’ailette est lui même porté à une température constante qL. Dans ce cas on obtient les expressions suivantes :
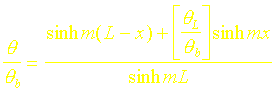
![]()
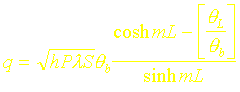
VI. Cas limite d’une ailette infinie
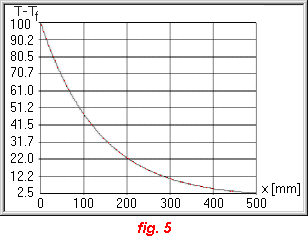
Dans le cas limite enfin où l’on peut considérer que l’ailette est infiniment longue et que la température du bout est la température du fluide ambiant, on a simplement :
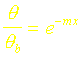
![]()
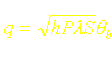
VII. Exercices :
1. Pour différentes ailettes de section uniforme et différents matériaux, calculer les flux évacués en fonction du coefficient d’échange h.
2. Dans le cas d’une ailette cylindrique, déterminer la longueur à partir de laquelle elle peut être assimilée à une ailette infinie.
3. Pour une masse donnée d’un matériau , déterminer le rayon optimum d’une ailette cylindrique pour lequel la déperdition est maximale.
![]()