I. INTRODUCTION

Les méthodes intégrales sont généralement utilisées dans le cas de transferts unidimensionnels linéaires ou non et peuvent être étendus aux problèmes avec changement de phase. Ces méthodes utilisent la notion de profondeur de pénétration d(t) définissant une couche thermique au delà de laquelle le flux de chaleur est pratiquement nul, entraînant à cette distance et au delà une température constante égale à la température initiale. Dans sa formulation une méthode intégrale utilise un distribution de température (généralement polynomiale) dans la couche thermique d'épaisseur d(t).

On rappelle d’abord dans ce chapitre les fondements mathématiques de la méthode. Une présentation du TP est ensuite proposée.

II. PROBLEME DU MUR SEMI-INFINI

Considérons l’équation de la chaleur dans un mur semi-infini:

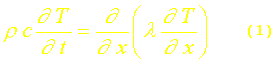
la condition initiale et les conditions aux limites sont:

Intégrons l’équation (1) de 0 à x:

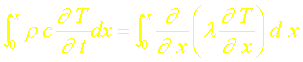
Le terme de droite de l’égalité précédente conduit à:

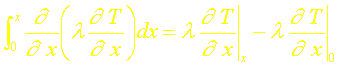
soit en introduisant les flux:

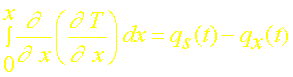
Le principe de la méthode intégrale consiste à supposer l’existence d’une profondeur de pénétration d(t) au delà de laquelle le signal thermique est encore nul. En x=d on a donc q_d(t)=0 et par conséquent l’équation précédente s’écrit:

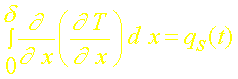
On en déduit finalement (si rc est constant):

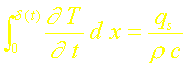
La formule de LEIBNITZ permet d’écrire:

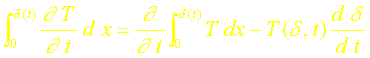
Sachant que T(d,t) = T_i, on obtient finalement:

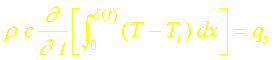
Cette équation intégrale traduit la conservation de l’énergie dans la couche [0,d]. Le choix d’un profil de température T(x) permet d’en déduire la profondeur de pénétration et par suite la température et le flux entrant dans le mur.

A. Cas d’un profil linéaire

Choisissons pour commencer un profil linéaire de la forme: T=ax+b, et utilisons les deux conditions:

T(0,t)=T_s        T(d,t)=T_i

On peut donc écrire {puisque T(d)=T_i}:

b=T_s        T_i=ad+T_s

soit:

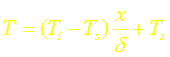
ce qui peut se mettre sous la forme:

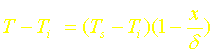
Injectons à présent ce profil dans l’équation intégrale:

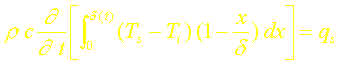
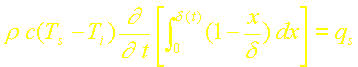
En effectuant les intégrations, on obtient:

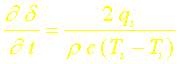
Or le flux surfacique s’écrit:

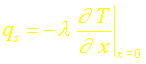
soit en calculant la dérivée:

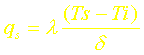
On a donc:

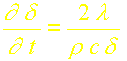
soit:

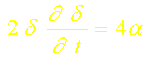
ou encore:

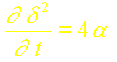
Cette équation s’intègre facilement et conduit finalement à la profondeur de pénétration:

Le flux de chaleur à la surface et le profil de température s’en déduisent:

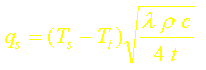
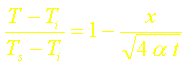
Rappelons que le flux surfacique exact s’écrit dans ce cas:

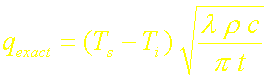
Le rapport du flux calculé par la méthode intégrale avec un profil de température uniforme au flux exact est donc:

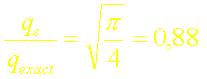
soit une erreur de 12%.

B. Cas d’un profil parabolique

Si l’on choisit un profil de température parabolique : T=a+bx+cx² et que l’on utilise les trois conditions suivantes:

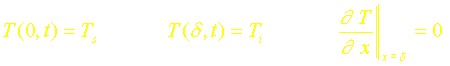
on montre que:

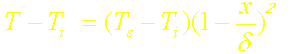
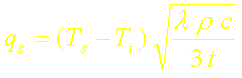
Le rapport du flux calculé par la méthode intégrale avec un profil de température parabolique au flux exact est ici:

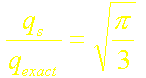
soit une erreur de 2,3%.

C. Cas d’un profil cubique

Dans le cas d’un profil cubique: T=a+bx+cx²+dx³, il nous faut une condition supplémentaire aux trois conditions déjà utilisées pour le profil parabolique. On peut alors choisir d’écrire la stationnarité de la température en x=0 ou en x=d soit:

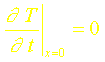
ou

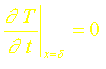
L’équation de la chaleur permet alors d’en déduire les deux conditions supplémentaires possibles:

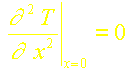
ou

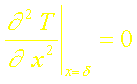
On obtient donc deux solutions possibles dans le cas du profil cubique. La première conduit à:

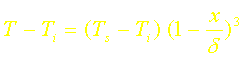
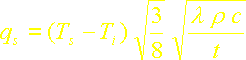
Le rapport du flux calculé par la méthode intégrale avec ce premier profil de température cubique au flux exact est ici:

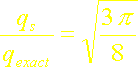
soit une erreur de 8,5 %.

L’utilisation de l’autre condition aux limites conduit quant à elle à:

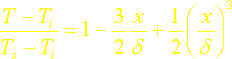
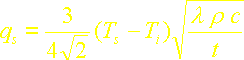
Le rapport du flux calculé par la méthode intégrale avec ce deuxième profil de température cubique au flux exact est ici:

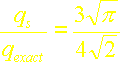
soit une erreur de 6 %.

D. Cas d'un profil polynomial d'ordre 4

Dans le cas d’un profil polynomial d’ordre 4 :T=a+bx+cx²+dx³+ex⁴, les deux conditions précédentes sont utilisées simultanément. On obtient alors:

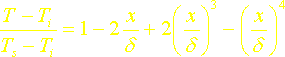
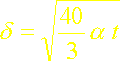
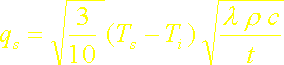
Le rapport du flux calculé par la méthode intégrale avec ce deuxième profil de température cubique au flux exact est ici:

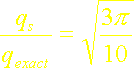
soit une erreur de 3 %.

III. PROFIL D’ORDRE GENERAL ET ETUDE ASYMPTOTIQUE

On s’intéresse dans cette partie au profil d’ordre général:

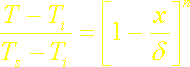
où n est un entier.

Ce profil vérifie les conditions T=T_s en x=0 et T=T_i en x=d. Il vérifie également les conditions suivantes:

Dans ce cas on obtient les expressions suivantes pour la profondeur de pénétration, la répartition de température et le flux surfacique:

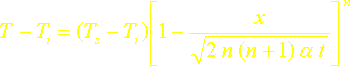
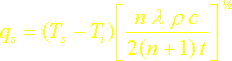
Le comportement de ces solutions en fonction de n fait l’objet d’un exercice numérique dont un déroulement possible est proposé ci-dessous.

IV. DEROULEMENT DU TP

v Etablir les relations précédentes

v Etude de la profondeur de pénétration : tracer d(t) pour différentes valeurs de n.

v Pour différentes valeurs de n, tracer T(t) à une abscisse donnée , T(x) à un instant donné et le flux surfacique.

v Effectuer une comparaison avec les solutions exactes. Conclure.

v Effectuer une étude asymptotique et montrer que:

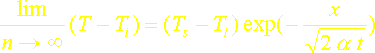
Annexe

On rappelle dans cette annexe la formule de LEIBNITZ qui permet d’évaluer la dérivée de l’intégrale.
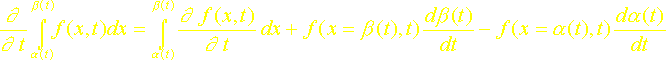