![]()
![]()
I. INTRODUCTION
La plupart des méthodes de mesure de la diffusivité thermique des solides isotropes sont basées sur des techniques impulsionnelles. Une des faces de l’ échantillon à étudier est soumise à un flux thermique (lumineux ou infrarouge) de très courte durée. Un suivi de l’évolution de la température permet alors de calculer la diffusivité.
Les simulations numériques proposées ici ont pour dut la mise en oeuvre et l’illustration des notions théoriques nécessaires à la modélisation du phénomène.
II. LE MODELE THERMIQUE
Considérons un mur d’épaisseur L de conductivité l de diffusivité a et de température initiale Tp. La face x=L est maintenue à la température constante Tp tandis que la face x=0 est soumise à un flux de chaleur q en créneau de durée to {figure 1}.
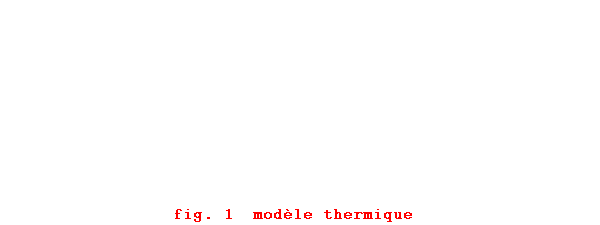
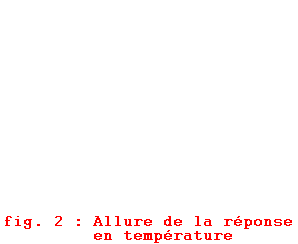
Quand le flux de chaleur est appliqué, la température en n’importe quel point du mur croît. Au bout d’un certain temps (dépendant de la position) après l’annulation du flux, la température passe par un maximum et décroît (Figure 2). La mesure du temps tmax où la température atteint son maximum permet de remonter à la diffusivité thermique a.
III. CALCUL DE LA SOLUTION ANALYTIQUE
Le calcul de la solution analytique est effectué en utilisant la méthode de séparation des variables et le principe de superposition des solutions.
A. Réponse à un flux constant
En effectuant le changement de variables q = T - Tp , l’équation de la chaleur et les conditions du problème s’écrivent :
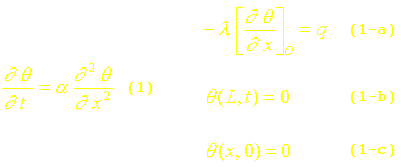
La méthode de séparation des variables n’est pas utilisable directement sur ce problème. Nous allons donc chercher la solution q sous la forme :
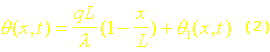
où
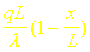
est la solution stationnaire.
La fonction q1(x,t) est solution du problème homogène suivant :
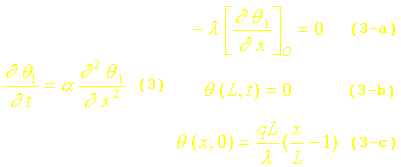
Séparons à présent les variables et posons :
![]()
L’injection de la forme (4) dans l’équation (3) conduit à :
![]()
soit :
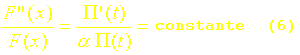
La température ne pouvant croître indéfiniment et ne pouvant avoir une allure sinusoïdale, la constante de l’équation (6) ne peut être que négative . On peut donc écrire :
constante=-b2
L’intégration des deux équations différentielles (6) conduit alors aux expressions :
![]()
![]()
En regroupant les constantes d’intégration, la fonction q1 s’écrit finalement :
![]()
Les constantes C1, D1 et b sont à présent déterminées grâce aux conditions aux limites et initiale.
1. Détermination des constantes C1 et b
La dérivée de q1 par rapport à x s’écrit :
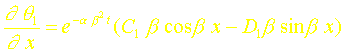
La condition (3-a) appliquée à l’équation précédente entraîne : C1=0
La deuxième condition aux limites s’écrit quant à elle :
![]()
La constante D1 ne pouvant être nulle (pour éviter la solution triviale q1=0), on doit donc avoir :
![]()
On obtient ainsi une infinité de solutions possibles pour la constante b:
![]()
A chaque valeur de b: correspond une solution possible du problème. La solution générale sera donc composée de l’ensemble de ces solutions:
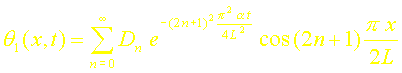
2. Détermination des constantes Dn
Il reste à déterminer les constantes Dn en utilisant la condition initiale (3-c) :
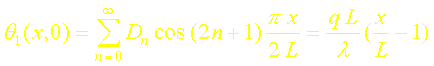
On reconnaît dans la relation précédente le développement en série de FOURIER (plus précisément en série de cosinus) de
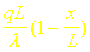
Les coefficients Dn sont donc simplement les coefficients de ce développement donnés par les relations :
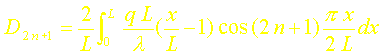
Sachant que :
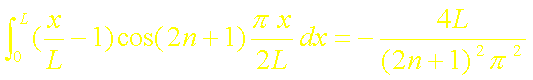
on a alors :
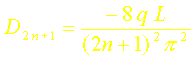
La fonction q1 s'écrit donc :
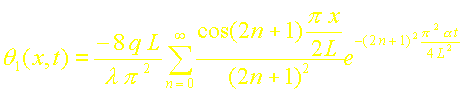
Finalement la solution du problème (1) est :
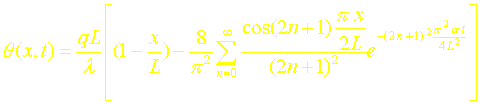
B. Réponse à un créneau de flux
La réponse au flux en créneau peut être déterminée par superposition. La figure 3 montre en effet que le flux imposé est la somme de deux échelons :
Si l’on désigne par E(t) la réponse à un flux de chaleur q constant, alors la réponse au flux en créneau sera E(t)-E(t-t0).
L’évolution de la température dans le mur suite à l’imposition du flux en créneau est donc donnée finalement par :
Ø t < to :
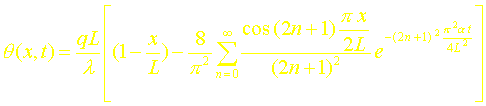
Ø t > to :
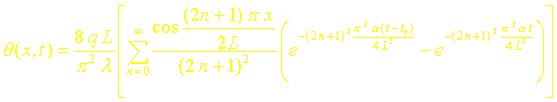
IV. DETERMINATION ANALYTIQUE DU MAXIMUM
Le temps au bout duquel la température atteint son maximum peut être déterminé en écrivant :
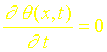
L’expression correspondant à t>to doit bien sûr être considérée ici. On obtient alors après dérivation :
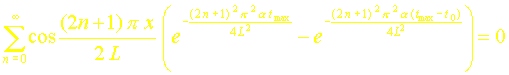
En introduisant les grandeurs adimensionnelles suivantes :
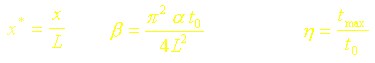
La relation précédente s’écrit :
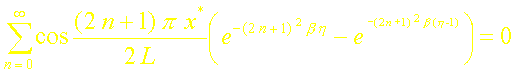
V. DETERMINATION APPROCHEE DU MAXIMUM
En ne gardant que les deux premiers termes de la série infinie précédente on obtient en x=L/2 :
![]()
Soit en multipliant par ebh:
![]()
ou encore :
![]()
On en déduit finalement la relation approchée suivante :
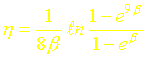
En revenant aux grandeurs physiques, on a donc :
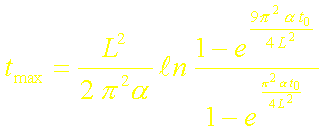
VI. EXPERIENCES NUMERIQUES
A. Evolution de la température et influence du nombre de termes de la série solution
Effectuer différentes simulations et tracer les courbes d’évolution de la température en différentes abscisses x=0, L/2, 3L/4 et x quelconque. Interpréter les résultats en introduisant la notion d’inertie thermique.
Vérifier qu’un nombre de termes faible est suffisant pour obtenir une valeur de tmax avec une précision suffisante.
Montrer en revanche qu’au voisinage de t=0, la série converge lentement. Le nombre de termes nécessaire est alors important.
Tracer à titre d’exemple l’évolution de la température entre 0 et 100 secondes en x=0,0025m pour la configuration suivante : q=50000W/m²; t0=50s; L =0,02m; l=0,03W/mK; r=1000Kg/m3; c=1950J/KgK (On prendra comme nombre de termes de la série les valeurs n = 100 et n = 1500).
Vérifier que tmax est indépendant de q.
B. Notion de constante de temps
Considérer les valeurs suivantes : q=20000W/m²; L=0,01m; t0=5s; l=384W/mK; r=1000Kg/m3; c=1950J/KgK
Tracer l’évolution de la température jusqu'à un temps de 10 secondes. Expliquer le phénomène. Conclusion.
C. Détermination de la diffusivité
Tracer les courbes h=f(b) données par le calcul exact et par le calcul approché. Comparer les résultats.
Comment peut-on utiliser cette courbe pour déterminer la diffusivité thermique ?
D. Détermination de la conductivité thermique
Montrer comment on peut déterminer la conductivité thermique.
![]()