I. INTRODUCTION

Le théorème de Duhamel permet de déterminer l'évolution des températures dans un milieu, sous l'influence de sollicitations variables dans le temps, si l'on connaît l'évolution des températures correspondant à des sollicitations constantes. Ce théorème utilise le caractère linéaire de l’équation de la chaleur quand les propriétés thermo-physiques du milieu sont indépendantes de la température. Ce théorème est illustré ici à travers l'exemple de la conduction dans un mur d'épaisseur L. Partant d'une approximation de l'évolution de la température en x=L/2 en réponse à une température constante imposée sur ses deux faces, nous traçons l'évolution de la température correspondant à une température imposée variant linéairement dans le temps, déterminée à l'aide du théorème de Duhamel.

Cette solution est comparée à la solution analytique exacte du problème. On montre ainsi que dans le domaine temporel de validité de l'approximation de la réponse à l'échelon, le théorème de Duhamel conduit à la bonne solution.

[la réponse à l'échelon utilisée dans ce TP est la réponse approchée d'ordre 1 étudiée dans le TP précédent.]

II. THEOREME DE DUHAMEL

Une formulation du théorème de Duhamel stipule que si F(x,t) représente la réponse à un échelon en température et que la température initiale est nulle, alors la réponse à une température variable f(t) s’écrit sous la forme du produit de convolution :

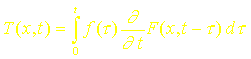
III. CAS D’UN MUR SOUMIS A UNE TEMPERATURE VARIANT LINEAIREMENT DANS LE TEMPS

A. Solution analytique exacte

En utilisant la transformation de Laplace, on peut montrer que la solution analytique exacte s’écrit :

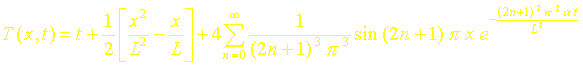
La solution en x=L/2 est donc :

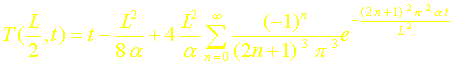
B. Détermination de la solution en utilisant le théorème de DUHAMEL

Nous allons utiliser à présent le théorème de Duhamel pour déterminer la solution de ce problème à partir de la réponse indicielle du premier ordre déterminée précédemment :

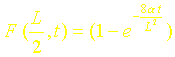
On a donc ici :

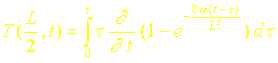
Le calcul de la dérivée conduit à :

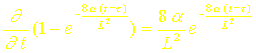
On a donc :

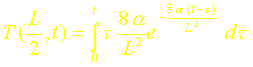
L’intégration étant effectuée par rapport à t, on a alors :

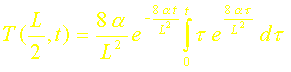
Or :

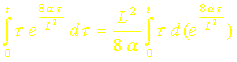
soit :

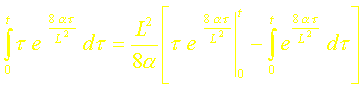
ou encore (après intégration) :

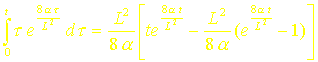
Ceci conduit à :

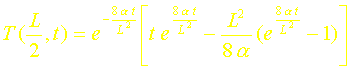
soit finalement :

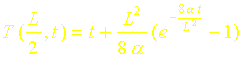
La validité de cette solution est bien évidemment liée au domaine de validité de la réponse à l’échelon que nous avons utilisée. On constate néanmoins que l’on retrouve la même valeur asymptotique que celle donnée par la solution analytique exacte.