![]()
![]()
I. INTRODUCTION
Soit une sphère de rayon R et de diffusivité a, initialement à une température Ti et qui est subitement portée en surface à une température Tb. On veut déterminer le temps de demi-chauffe t qui est le temps nécessaire pour que l’écart entre la température en un point de la sphère et la température imposée soit divisé par deux. On utilise pour cela la solution analytique du problème et une solution approchée conduisant à une expression analytique simple du temps de demi-chauffe. Le domaine de validité de la solution approchée est finalement déterminé.
II. SOLUTION ANALYTIQUE DU PROBLEME
La solution analytique exacte du problème schématisé dans la figure 1 est :
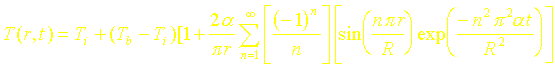
Le temps de demi-chauffe t est défini quant à lui par la relation :
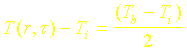

A partir de la solution analytique précédente, le temps de demi-chauffe est calculé par le logiciel.
III. CALCUL DU TEMPS DE DEMI-CHAUFFE APPROCHE
La définition du temps de demi-chauffe conduit à l’expression :
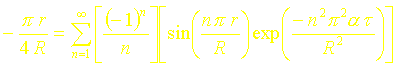
En tronquant la série à l’ordre 1, on obtient :
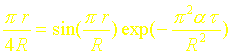
Soit :
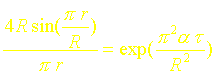
En prenant le logarithme de l’expression précédente on a :
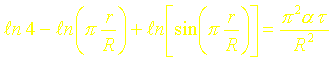
Utilisons l’approximation suivante :
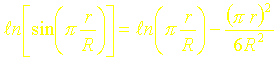
On obtient finalement :
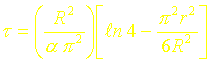
IV. DEROULEMENT DU TP
On propose dans cette partie un déroulement possible de ce TP.
A. La solution analytique
1. évolution de la température
Tracer la courbe T(t) en plusieurs rayons et en considérant plusieurs cas :
Ø Sphères de différents rayons
Ø Différents matériaux (conducteurs et isolants)
Ø Etudier l’influence du nombre de termes de la série
2. profondeur de pénétration
Tracer la courbe T (r) représentant la répartition de la température dans la sphère à plusieurs instants t. Considérer ici aussi plusieurs matériaux.
Déterminer la profondeur de pénétration d (t) en fonction du temps. On prendra comme définition de la profondeur de pénétration la profondeur au delà de laquelle la température est inférieure à un pourcentage faible (par exemple 1%) de la température de surface.
B. Le choix des unités
Le programme est prévu pour utiliser les unités du système internationale {SI} : R en [m] ,T en [s] et a en [m²/s] .En conséquence , les légendes graphiques sont exprimées dans ces unités .On peut cependant effectuer les calculs avec d’autres unités .
1. changement d’unités
On peut choisir par exemple de travailler avec R en [cm] et t en [h] , soit a en [cm²/h]. La correspondance est dans ce cas :
Ø 1 m²/s = 2.77 cm²/h
Ø 1cm²/h = 0 .36 m²/s
Les deux jeux de paramètres suivants conduiront donc aux même résultats :
Ø R = 1 cm ; a = 0.1 cm²/h (l = 0.01, r = c = 1)
Ø R = 0.01 m ; a = 0.0036 m²/s (l = 36, r = c = 100)
Effectuer des simulations (pour les mêmes cas réels) avec les deux systèmes d’unités précédents. Conclure.
2. grandeurs adimensionnelles
On peut introduire les grandeurs adimensionnelles suivantes :
r* = r /R , t* = at / R² et q =(T - To)/(Tp - To)
Effectuer une simulation adimensionnelle et comparer les résultats obtenus aux résultats de l’étude dimensionnelle. Conclure.
C. Le temps de demi-chauffe exact
Tracer t1/2 = f ( r /R ) puis t1/2 = f ( r² /R² ) pour différents matériaux. En déduire l’existence de deux régions distinctes (une région de variation linéaire en r²/ R² et une région non linéaire ).
Remarque : les temps de calcul de cette partie sont importants.
Déterminer graphiquement l’ordonnée à l’origine et la pente de la partie linéaire et les comparer aux valeurs approchées.
D. Le temps de demi-chauffe approché
Tracer t1/2 = f ( r /R ) puis t1/2 = f ( r² /R² ) pour différents matériaux. Déterminer le rayon adimensionnel au delà duquel t 1/2 devient négatif.
Comparer les courbes obtenues avec les courbes de la partie {IV.C.}
Effectuer une étude adimensionnelle du temps de demi-chauffe.
Conclusions.
![]()